반응형
2001학년도 대학수학능력시험 수학(인문계)
시행 : 2000.11.15(수)
대상 : 고등학교 3학년
출제 : 교육과정평가원
2000-11 고3 수능 2수학(인문계)[문제].pdf
0.46MB
2000-11 고3 수능 2수학(인문계)[정답].pdf
0.02MB
2000-11 고3 수능 2수학(인문계)[해설].pdf
0.32MB











삽화, 사진, 표는 누락되어 있습니다. 원본 파일을 참고하시기 바랍니다.
1. $\left( \sqrt{2} \right)^{5}$의 값은?
① $\sqrt{2}$
② $2$
③ $2 \sqrt{2}$
④ $4$
⑤ $4 \sqrt{2}$
2. 이차방정식 $x^{2} +7x+1=0$의 두 근이 $\alpha$, $\beta $일 때, $$( \alpha^{2} + \beta^{2} )+7( \alpha + \beta )$$의 값은?
① $-4$
② $-2$
③ $0$
④ $1$
⑤ $3$
3. $\left(2+2\sin \dfrac{\pi}{3} \right)\left(2-\tan \dfrac{\pi}{3} \right)$의 값은?
① $1$
② $\dfrac{1}{2}$
③ $\dfrac{1}{3}$
④ $\dfrac{1}{4}$
⑤ $\dfrac{1}{5}$
4. $f(x)=x^{5} +x$일 때, $f^{\prime} (1)$의 값은?
① $1$
② $2$
③ $5$
④ $6$
⑤ $12$
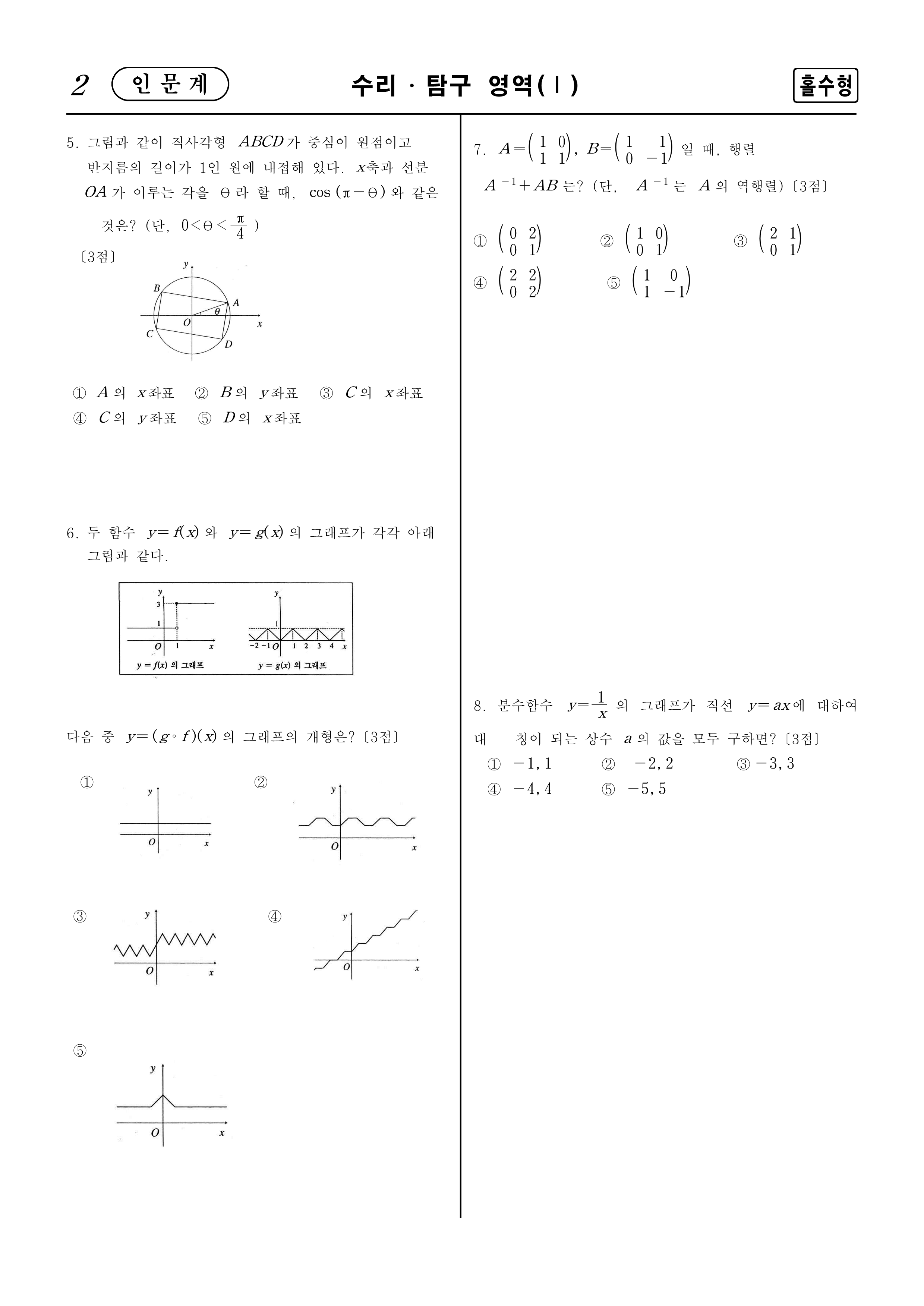
5. 그림과 같이 직사각형 $ABCD$가 중심이 원점이고 반지름의 길이가 $1$인 원에 내접해 있다. $x$축과 선분 $OA$가 이루는 각을 $\theta $라 할 때, $\cos ( \pi - \theta )$와 같은 것은? (단, $0 < \theta < \dfrac{\pi}{4}$)
① $A$의 $x$좌표
② $B$의 $y$좌표
③ $C$의 $x$좌표
④ $C$의 $y$좌표
⑤ $D$의 $x$좌표
6. 두 함수 $y=f(x)$와 $y=g(x)$의 그래프가 각각 아래 그림과 같다.
다음 중 $y=(g \circ f )(x)$의 그래프의 개형은?
7. $A= \begin{pmatrix}1&0\\1&1\end{pmatrix}$, $B= \begin{pmatrix}1&1\\0&-1\end{pmatrix}$일 때, 행렬 $A^{-1} +AB$는? (단, $A^{-1}$는 $A$의 역행렬)
① $\begin{pmatrix}0&2\\0&1\end{pmatrix}$
② $\begin{pmatrix}1&0\\0&1\end{pmatrix}$
③ $\begin{pmatrix}2&1\\0&1\end{pmatrix}$
④ $\begin{pmatrix}2&2\\0&2\end{pmatrix}$
⑤ $\begin{pmatrix}1&0\\1&-1\end{pmatrix}$
8. 분수함수 $y= \dfrac{1}{x}$의 그래프가 직선 $y=ax$에 대하여 대칭이 되는 상수 $a$의 값을 모두 구하면?
① $-1$, $1$
② $-2$, $2$
③ $-3$, $3$
④ $-4$, $4$
⑤ $-5$, $5$
9. 반지름의 길이가 $r$이고 높이가 $1$인 원기둥에 물이 들어있다. 원기둥을 수평으로 뉘었을 때 수면과 옆면이 만나서 이루는 현에 대한 중심각을 $\theta $라 하자. 원기둥을 세웠을 때 수면의 높이 $h$를 $\theta $로 표시하면? (단, $0 < \theta < \pi$, $0 < h < \dfrac{1}{2}$)
① $h= \dfrac{1}{2 \pi} \theta $
② $h= \dfrac{1}{2 \pi} \sin \theta $
③ $h= \theta -\sin \theta $
④ $h= \dfrac{1}{2 \pi} ( \theta +\sin \theta )$
⑤ $h= \dfrac{1}{2 \pi} ( \theta -\sin \theta )$
10. 구간 $[0, 1]$에서 정의된 연속확률변수 $X$의 확률밀도함수가 $f(x)=ax+a$로 주어졌을 때, 상수 $a$의 값은?
① $\dfrac{1}{3}$
② $\dfrac{2}{3}$
③ $1$
④ $\dfrac{3}{2}$
⑤ $2$
11. 삼차함수 $y=f(x)$가 서로 다른 세 실수 $a$, $b$, $c$에 대하여 $$f(a)=f(b)=0,\,\,\,\,f^{\prime} (a)=f^{\prime} (c)=0$$을 만족시킨다. $c$를 $a$와 $b$로 나타내면?
① $a+b$
② $\dfrac{a+b}{2}$
③ $\dfrac{a+b}{3}$
④ $\dfrac{a+2b}{3}$
⑤ $\dfrac{2a+b}{3}$
12. 그림과 같이 이웃한 두 교차로 사이의 거리가 모두 $1$인 바둑판 모양의 도로망이 있다. 두 차량이 각각 $A$와 $B$에서 출발하여 $A$, $B$ 이외의 교차로 $P$에서 만났다. 두 차량이 움직인 거리의 합이 $4$가 되는 $P$의 위치를 모두 표시하면?
13. 다음은 좌표평면 위의 서로 다른 네 점 $A$, $B$, $C$, $D$에 대한 설명이다.
㈎ 점 $A$와 점 $B$는 $x$축 위에 있다.
㈏ 점 $B$의 $x$좌표는 점 $A$의 $x$좌표보다 크다.
㈐ $\overline{AB} = \overline{AC} = \overline{BC} = \overline{AD} = \overline{CD}$
㈏ 점 $B$의 $x$좌표는 점 $A$의 $x$좌표보다 크다.
㈐ $\overline{AB} = \overline{AC} = \overline{BC} = \overline{AD} = \overline{CD}$
점 $A$, $B$, $C$, $D$의 $x$좌표를 각각 $a$, $b$, $c$, $d$라 할 때, 옳은 것은?
① $a < d < c < b$
② $c < a < d < b$
③ $c < d < a < b$
④ $d < a < c < b$
⑤ $d < c < a < b$
14. 좌표평면의 제$1$사분면 위의 점 $P$에서 $x$축, $y$축에 내린 수선의 발을 각각 $Q$, $R$라 하자. 점 $A(-1, -1)$에 대하여 $\overline{PA} = \overline{PQ} + \overline{PR}$를 만족시키는 점 $P$의 자취의 개형은?
15. 자연수 $n$에 대하여 $n^{2}$을 오진법으로 표현했을 때 일의 자리 수를 $f(n)$이라 하자. [보기] 중 옳은 것을 모두 고르면?
<보 기>
ㄱ. $f(3)=4$
ㄴ. $0 \le f(n) \le 4$
ㄷ. $f(n)=2$인 자연수 $n$은 없다.
ㄴ. $0 \le f(n) \le 4$
ㄷ. $f(n)=2$인 자연수 $n$은 없다.
① ㄱ
② ㄴ
③ ㄱ, ㄷ
④ ㄴ, ㄷ
⑤ ㄱ, ㄴ, ㄷ
16. 전체집합 $U= \left\{ 1, 2, 3, 4, 5 \right\}$의 서로 다른 두 부분집합 $X$, $Y$에 대하여 $(X \cup Y )-(X \cap Y )$의 가장 작은 원소가 $X$에 속할 때, $X⇨Y$라 하자. $U$의 부분집합 $A= \left\{ 2, 3, 4 \right\}$, $B= \left\{ 1, 2, 5 \right\}$, $C= \left\{ 2, 4, 5 \right\}$에 대하여 옳은 것은?
① $A⇨B⇨C$
② $A⇨C⇨B$
③ $B⇨A⇨C$
④ $B⇨C⇨A$
⑤ $C⇨A⇨B$
17. 다음은 지수법칙 $a^{r+s} =a^{r} a^{s}$으로부터 모든 양수 $x$, $y$에 대하여 $$\log_{a} xy=\log_{a} x+\log_{a} y$$ 가 성립함을 증명한 것이다. (단, $a \ne 1$, $a > 0$)
<증 명>
$r=\log_{a} x$, $s=\log_{a} y$로 놓으면
$$a^{r} =x,\,\,\,\,a^{s} =\fbox{ ㈎ }$$
지수법칙으로부터 $a^{r+s} =\fbox{ ㈏ }$
로그의 정의에 의하여 $r+s=\log_{a}\fbox{ ㈏ }$
그러므로 $\log_{a} xy=\log_{a} x+\log_{a} y$이다.
로그의 정의에 의하여 $r+s=\log_{a}\fbox{ ㈏ }$
그러므로 $\log_{a} xy=\log_{a} x+\log_{a} y$이다.
위의 증명에서 ㈎, ㈏에 알맞은 것을 순서대로 적으면?
① $x$, $x+y$
② $y$, $x+y$
③ $x$, $xy$
④ $y$, $xy$
⑤ $x$, $\dfrac{x}{y}$
18. 다음은 $\triangle ABC$에서 $\overline{BC} < \overline{AC} < \overline{AB}$일 때, 삼각형 내부의 한 점 $P$에 대하여 $\overline{PA} + \overline{PB} + \overline{PC} < \overline{AB} + \overline{AC}$임을 증명한 것이다.
<증 명>
가정에 의해 $\overline{BC} < \overline{AC} < \overline{AB}$이므로
$\angle A < \angle B < \angle C$
점 $P$를 지나고 선분 $BC$에 평행한 직선이 선분 $AB$, $AC$와 만나는 점을 각각 $D$, $E$라고 하자.
선분 $DE$와 선분 $BC$가 평행하므로 $$\angle ADE= \angle B,\,\,\,\,\angle AED= \angle C$$ 따라서, $\angle A < \angle ADE < \angle AED$
그러므로 $\triangle ADE$에서 $\fbox{ ㈎ }$ $\cdots$ ①
이고 $\overline{PA} < \overline{AD}$ $\cdots$ ②
$\triangle BDP$에서 $\overline{PB} < \overline{PD} + \overline{DB}$ $\cdots$ ③
$\triangle EPC$에서 $\overline{PC} < \overline{PE} + \overline{EC}$ $\cdots$ ④
①, ②, ③, ④에서 $\overline{PA} + \overline{PB} + \overline{PC} < \overline{AB} + \overline{AC}$
위의 증명에서 ㈎에 알맞은 것은?
① $\overline{AD} < \overline{AE} < \overline{DE}$
② $\overline{AD} < \overline{DE} < \overline{AE}$
③ $\overline{AE} < \overline{AD} < \overline{DE}$
④ $\overline{AE} < \overline{DE} < \overline{AD}$
⑤ $\overline{DE} < \overline{AE} < \overline{AD}$
19. $0 < \theta < \dfrac{\pi}{2}$일 때, $\log (\sin \theta )-\log (\cos \theta )= \dfrac{1}{2} \log 3$을 만족시키는 $\theta $의 값은? (단, $\log $는 상용로그)
① $\dfrac{1}{6} \pi $
② $\dfrac{1}{4} \pi $
③ $\dfrac{2}{7} \pi $
④ $\dfrac{1}{3} \pi $
⑤ $\dfrac{2}{5} \pi $
20. 좌표평면 위에 여섯 개의 점 $(1, 1)$, $(1, -1)$, $(0, 1)$, $(0, -1)$, $(-1, 1)$, $(-1, -1)$이 있다. 이 중 세 점을 지나는 이차함수 $y=f(x)$의 개수는?
① $2$
② $4$
③ $6$
④ $8$
⑤ $10$
21. 다음은 정적분 $\displaystyle\int_{0}^{1} (x^{2} +1)dx$의 근사값의 오차의 한계를 구하는 과정의 일부이다.
그림 ㈎, ㈏와 같이 폐구간 $\left[ 0, 1 \right]$을 $n$등분하여 얻은 $n$개의 직사각형들의 넓이와 합을 각각 $A$, $B$라 하자. $A-B \le 0.15$가 되는 $n$의 최소값은?
① $6$
② $7$
③ $8$
④ $9$
⑤ $10$
22. 영어의 알파벳 $A$, $B$, $\cdots$, $Z$에 십진법의 수 $1$부터 $26$에 해당하는 이진법의 수 $00001_{(2)}$, $00010_{(2)}$, $\cdots$, $11010_{(2)}$을 순서대로 대응시키자. 이진법의 수 $\alpha $와 $\beta $의 각 자리의 수를 비교하여 같으면 $0$, 다르면 $1$을 그 자리에 대응시켜 얻은 이진법의 수를 $\alpha \land \beta $라 하자. 예를 들면 $$10001_{(2)} \land 10101_{(2)} =00100_{(2)},\,\,\,\,00001_{(2)} \land 10101_{(2)} =10100_{(2)}$$ 각 알파벳에 대응하는 이진법의 수를 $10101_{(2)}$과 연산 $\land $을 하여 얻은 이진법의 수로 그 알파벳을 암호화하였다. 예를 들면 암호가 $10100_{(2)}$인 알파벳은 $A$이다. 암호가 $11001_{(2)}$인 알파벳은?
① $B$
② $D$
③ $L$
④ $P$
⑤ $S$
23. 좌표평면 위의 네 점 $(-2, 2)$, $(4, 2)$, $(1, -2)$, $(4, -2)$에 있는 나사를 모두 조이는 작업을 반복하는 로봇팔의 한쪽 끝을 점 $P$에 고정시키려 한다. 로봇팔은 점 $P$를 중심으로 $360˚$ 회전 가능하고, 점 $P$로부터의 거리가 로봇팔의 길이 이하인 모든 곳의 나사를 조일 수 있다. 로봇팔의 길이를 최소로 할 수 있는 점 $P$의 좌표는?
① $(0, 0)$
② $(0, 1)$
③ $(0, -1)$
④ $(1, 0)$
⑤ $(1, 1)$
24. 다음은 세게 석유 소비 증가 추세에 관한 글들이다.
$\cdots$ 매년 석유 소비량을 조사한 결과, 최근 10년 동안 소비된 석유의 양은 그 이전까지 소비된 석유의 양과 같다. 예를 들어 1981년부터 1990년까지 소비된 석유의 양은 1980년까지 소비된 석유 전체의 양과 같다. $\cdots$
이와 같은 석유 소비 추세가 계속된다고 가정하고, 현재까지 소비된 석유의 양을 $a$, 현재의 석유의 매장량을 $b$라 할 때, 앞으로 몇 년 동안 석유를 사용할 수 있겠는가?
① $10\log_{2} \left( \dfrac{b}{2a} +1\right)$
② $10\log_{2} \left( \dfrac{b}{a} +1\right)$
③ $10\log_{2} \left( \dfrac{2b}{a} +1\right)$
④ $10\log_{2} \left( \dfrac{b}{a} +2\right)$
⑤ $10\log_{2} \left( \dfrac{2b}{a} +2\right)$
25. 삼차함수 $f(x)=ax^{3} +b$의 역함수 $f^{-1}$가 $f^{-1} (5)=2$를 만족시킬 때, $8a+b$의 값을 구하시오.
26. 다항식 $f(x)$를 $(x-1)(x-2)$로 나눈 나머지가 $4x+3$일 때, $f(2x)$를 $x-1$로 나눈 나머지를 구하시오.
27. 다항함수 $f(x)$에 대하여 $\displaystyle\lim_{x \to 1} \dfrac{8(x^{4} -1)}{(x^{2} -1)f(x)} =1$일 때, $f(1)$의 값을 구하시오.
28. 문자 $a$, $b$, $c$에서 중복을 허용하여 세 개를 택하여 만든 단어를 전송하려고 한다. 단, 전송되는 단어에 $a$가 연속되면 수신이 불가능하다고 하자. 예를 들면 $aab$, $aaa$ 등은 수신이 불가능하고 $bba$, $aba$ 등은 수신이 가능하다. 수신 가능한 단어의 개수를 구하시오.
29. 함수 $f(x)$가 $f(10)=50$, $f(1)=3$을 만족시킬 때, $$\displaystyle\sum_{k=1}^{9} f(k+1)- \displaystyle\sum_{k=2}^{10} f(k-1)$$ 의 값을 구하시오.
30. 정적분 $\displaystyle\int_{0}^{1} (x+1) (x^{2} -x+1) dx$의 값을 소수점 아래 둘째 자리까지 구하시오.
'고3 > 수학' 카테고리의 다른 글
| 2001-11 고3 수능 수학(예체능계) (0) | 2023.02.08 |
|---|---|
| 2000-11 고3 수능 수학(자연계) (0) | 2023.02.08 |
| 2000-11 고3 수능 수학(예체능계) (0) | 2023.02.08 |
| 1999-11 고3 수능 수학(자연계) (0) | 2023.02.07 |
| 1999-11 고3 수능 수학(인문계) (0) | 2023.02.07 |